抗干扰二元编码原理及方法

[TOC]

4.1 抗干扰编码的基本原理

4.1.1 编码和纠错能力的关系

1. 只检测e个错：最小码距：$d_{min} >=e+1$

   助记：假设就检测一个错，而最小码距是1，那根本无法检测错误，因此至少e+1

   解释:

</div>

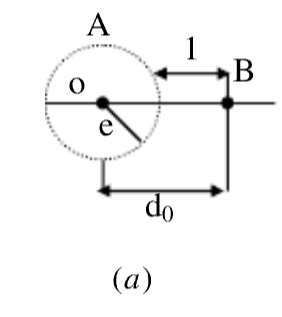
设一码组A位于O点，另一码组B与A最小码距为d0。当A码组发生e个误码时，可以认为A的位置将移动到以O为圆心、以e为半径的圆上，但其位置不会超出此圆。只要e比d0小1，发生个错码后错成的码组不可能变成另一任何许用码组，即有d>=e+1。

1. 纠正t个错:$d_{min} >= 2t +1$

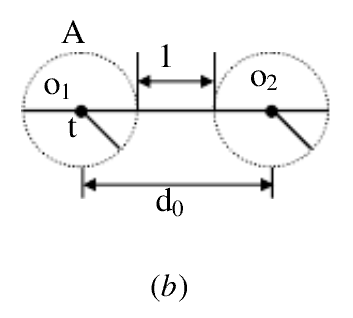
助记：我想纠正t个错，那码距如果是2t，将会纠错困难，信宿收到了A，字母表B和C距A都是t，那把B译成C还是A？那么要让$d_{min}$ 再多一位，那么B和C肯定有一个距A更小，则将A译成它。

解释:

例如：

$\sum : B,C \; $

B：1111 C：0000 $d_{min} = 4$

A：1100 无法纠错

码距+1： B：11111 C：00000

A: 11100 / 11000 均能纠错

1. 纠正t个错，检测e个错：$d_{min} >= t+e+1 (e>t) $

在解释此式之前，先来说明什么是“纠正个错码，同时又检测e个错码” （简称纠检结合）。在某些情况下，要求对于出现较频繁但错码数很少的码组按前向纠错方式工作，以

节省反馈重发时间,同时又希望对一些错码数较多的码组,在超过该码的纠错能力时,能自动按检错重发方式工作,以降低系统的总误码率。这种工作方式就是“纠检结合”

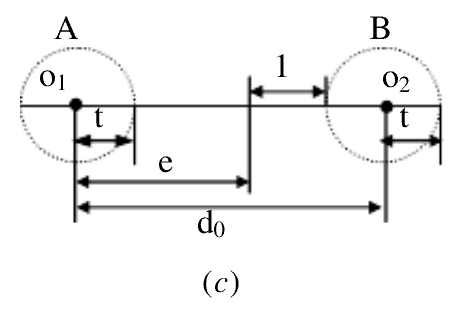
在上述“纠检结合”系统中，差错控制设备按照接收码组与许用码组的距离自动改变工作方式。若接收码组与某一许用码组间的距离在纠错能力t的范围内，则将按纠错方式工作，否则按检错方式工作。若设码组的检错能力为e,则当码组存在e个错码时,该码组与任一许用码组B的距离至少应有t+1,否则将进入许用码组B的纠错能力范围内，而被错纠为B，这就要求最小码距应满足图(c)。

4.1.2 抗干扰编码的基本原理

山农编码定理 ->

码组足够长时，存在一种编码方法，使增加的监督码元与原来的信息码元相比趋于任意小，效率

$\displaystyle\eta = \frac{R}{C}\to 1$

代数编码：监督码由信息码按一定算法给出。 分为分组码和卷积码。

• 分组码

1. k信息+r监督= n -> (n,k)码

2. $\displaystyle\eta = \frac{k}{n}$

3. 系统码： 监督位都在后面

• 卷积码

1. k个信息码输入到一个时序逻辑电路，输出与前m组输入的k有关：

$m’k+k = (m’+1)k = mk$

1. m -> 编码约束度

$n_总$ = m * n = (m’+1)* n

$\displaystyle\eta = \frac{k}{n}$

4.2 构造检错码

4.2.1 奇偶校验码

1. (n,n-1)码

   效率 $\displaystyle\eta = \frac{n-1}{n} $

2. 漏检概率

   奇偶校验码不能发现偶数错误： （$p_e : 误码率$)

   n为偶数：

   $p = \displaystyle\sum\limits_{i=1}^{n/2} C_{n}^{2i} p_{e}^{2i} (1-p_e)^{n-2i} \to p\approx\displaystyle\sum\limits_{x=1}^n C_n^xp_e^x 保留第一项得 p = C_n^2p_e^2 $

   n为奇数：

   $p= \displaystyle\sum\limits_{i=1}^{(n-1)/2} C_{n}^{2i} p_{e}^{2i} (1-p_e)^{n-2i}$

   $由于p_e «1，上面近似为 p \approx C_n^2p_e^2$

3. 例题： 4.4 (8,7)奇偶校验码的漏检概率和编码效率( $p_e = 10^{-4}$)

   ​ 7/8 ; $C_8^2 p_e^2$

4.2.2 定比码

——又叫等重码，1的个数为码的重量

53定比->与10个十进制数字对应，4个10进制数字代表一个汉字，于是可用于汉字编码

​ $C_5^3 = 10个许用码字，22个禁用$

73定比-> 对英文字母和键盘操作编码 $C_7^3=35个许用码字，2^7-C_7^3 = 93个禁用码字$

效率 $\displaystyle\eta = \frac{R}{C} ,R为每个码元的平均信息量，C为每个符号最大信息量$

53定比，许用10码字，若等概率分布，每个码字平均信息量= lb($C_{5}^3$),每个码元的平均信息量则为lb(*)/5 = 0.66 bit/signal

二元信源每个符号最大信息量为1bit/signal

所以 $\eta = 66 \%$

73类似

1. ARQ - Automatic Request for Repeat 检测到错误重发

4.3 构造纠错码

4.3.1 简单重复码

发 001100 -> 三重重复码 000，000，111，111，000，000

n重重复码 : 效率 = 1/n

4.3.2 汉明码 - 纠正1位错误

1. $2^r = n+1 \to 狭义汉明码 ，2^r >n+1 广义汉明码$
2. 监督矩阵[H]，确定信息码元和监督码元的关系
3. 生成矩阵[G],信息码A右乘G即得系统码B 掌握H、G的互换
4. 错误接受概率(实际误码率) $p = 1- [ (1-p_e)^n + C_n^1 p_e (1-p_e)^{n-1}]$

$p_e = 10^{-4} 时 p_{(7,4)} \approx 4.2* 10^{-7}$

1. $\eta = k/n =4/7 \approx 57\%$

4.3.3 CRC 循环冗余校验码

​ —— Cyclic Redundancy Check

1. 循环码是分组码 (n,k) 这里只讨论线性循环码

2. 码字 <=> 多项式 左乘$x^c$模($x_n+1$) <=> 左移c位 涉及模二运算

3. 生成多项式->生成矩阵->解决循环码编码

   定理： (n,k)循环码生成多项式g(x) 是 $x^n -1 的r次(n-k)因式$

4. 根据生成多项式$g(x) = x^3+x+1$ (1011)通过两种方法求循环码的码字表：

   • 求生成矩阵[G]

     [1011000,

     0101100,

     0010110,

     0001011]

     信息码 A(1:k) * G(k,n) -> 非系统码 B(1:n)

   • 直接利用g(x)：

     信息码A(x)

     $x^{n-k}A(x) = yg(x) + r(x)$

     B(x) = A(x) + r(x)

5. 根据一个特定循环码字可求出所有校验子

求传输错误后的B(x)’ = B(x) + e(x)

把B(x)’ mod $g(x)$ , e(x)即为校验子