[TOC]

Neural Code

课程的第一个部分，由于神经科学在理解大脑处理感官信息方面比较成熟，因此将从这一方面入手。

• technique for recording from the brain(fMRA…)
• tools discovering how brain represent information
• model express our understanding of this representation
• some methods for inferring what the brain is doing based on its activity(in w3)
• using information theory to quantify neural representation(in w4)
• biophysical basis of how the brain process inputs and performs complex computations(in w5)

Recording

outside the cell:

• fMRI
• EEG ——electroencephalography
  • faster response

both of them have the same shortage: can not recode one single neuron’s activity but an average of millons’

some ways to read single neuron:

• electrode arrays
• calcium imaging 钙离子荧光染色？神经冲动时钙离子内流，荧光强度代表活动强度

looking inside single cells:

• patch electrodes

  direct contact with inside of the cell

what is the neural code？

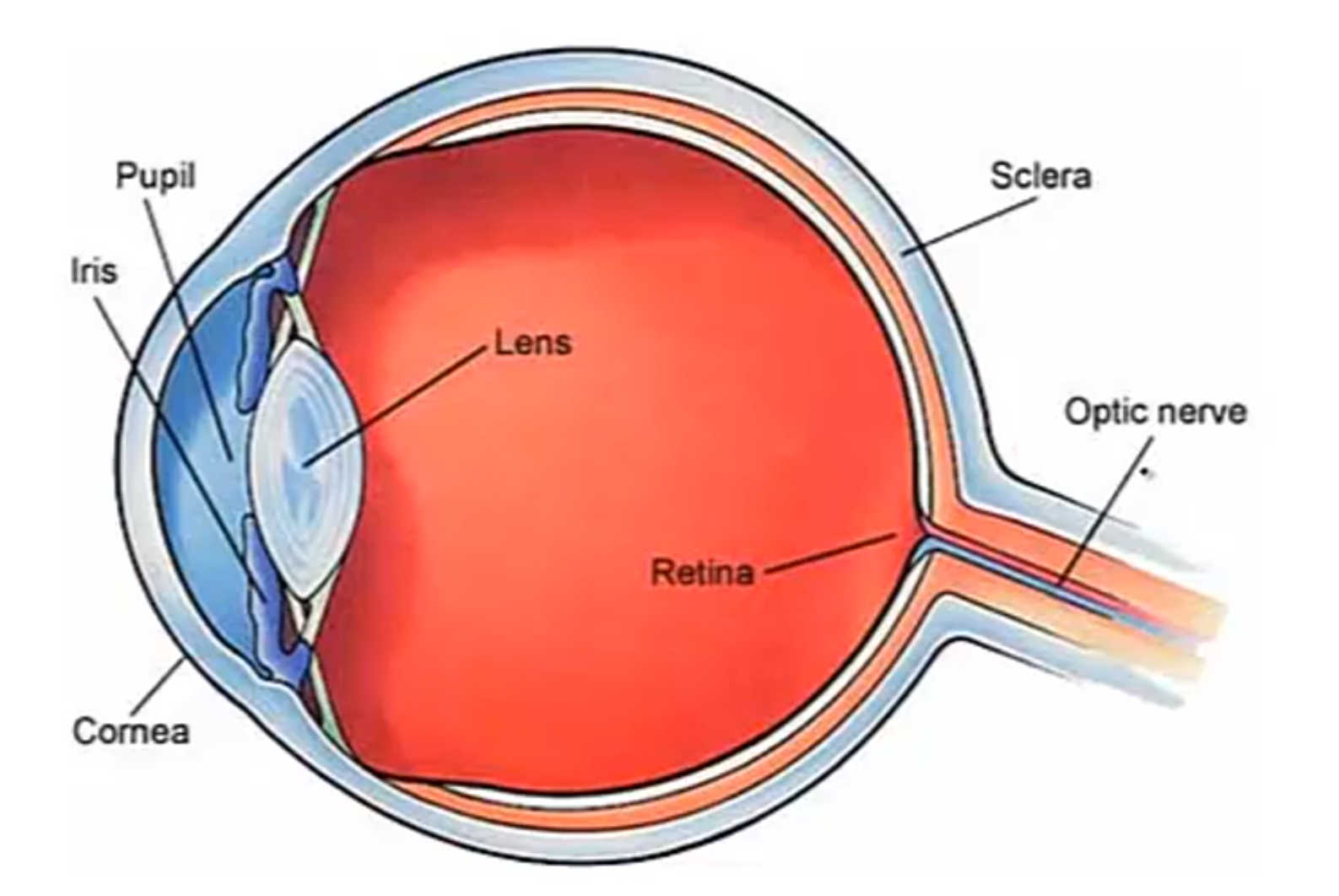
• cells in retina transfer the light signals to the electrical signals

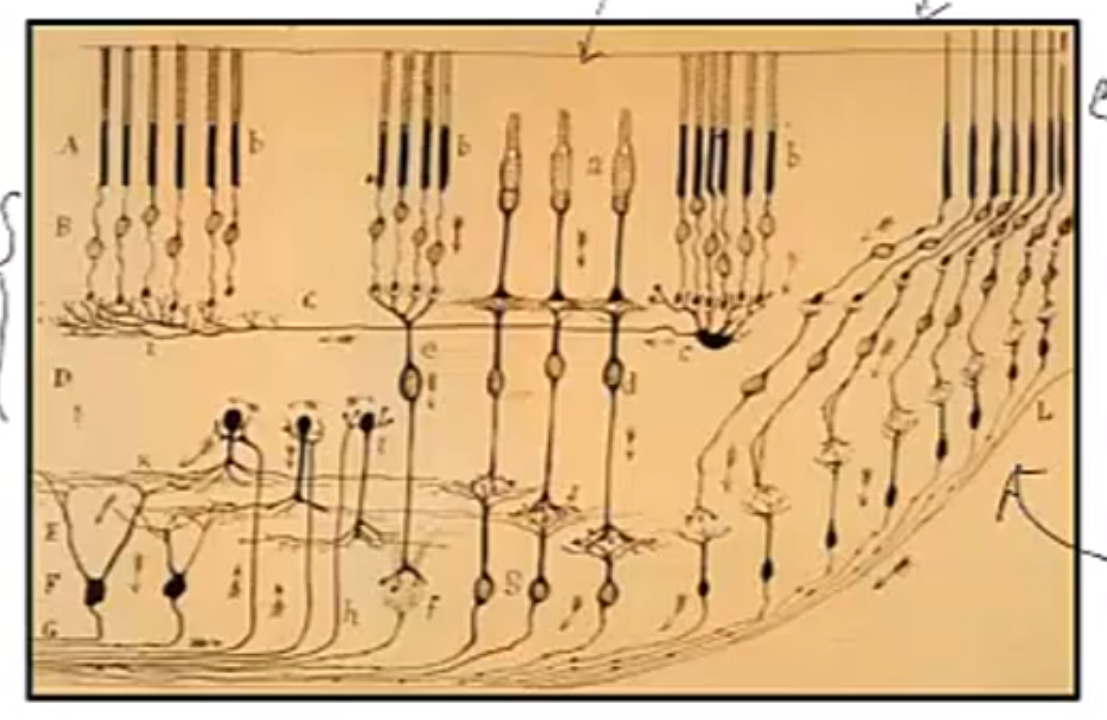
[input]photoreceptors(rods and columns) ->successive layers of cells->[output]retinal ganglion cells->optic track(视神经束)->rest of the brain

一个实验：

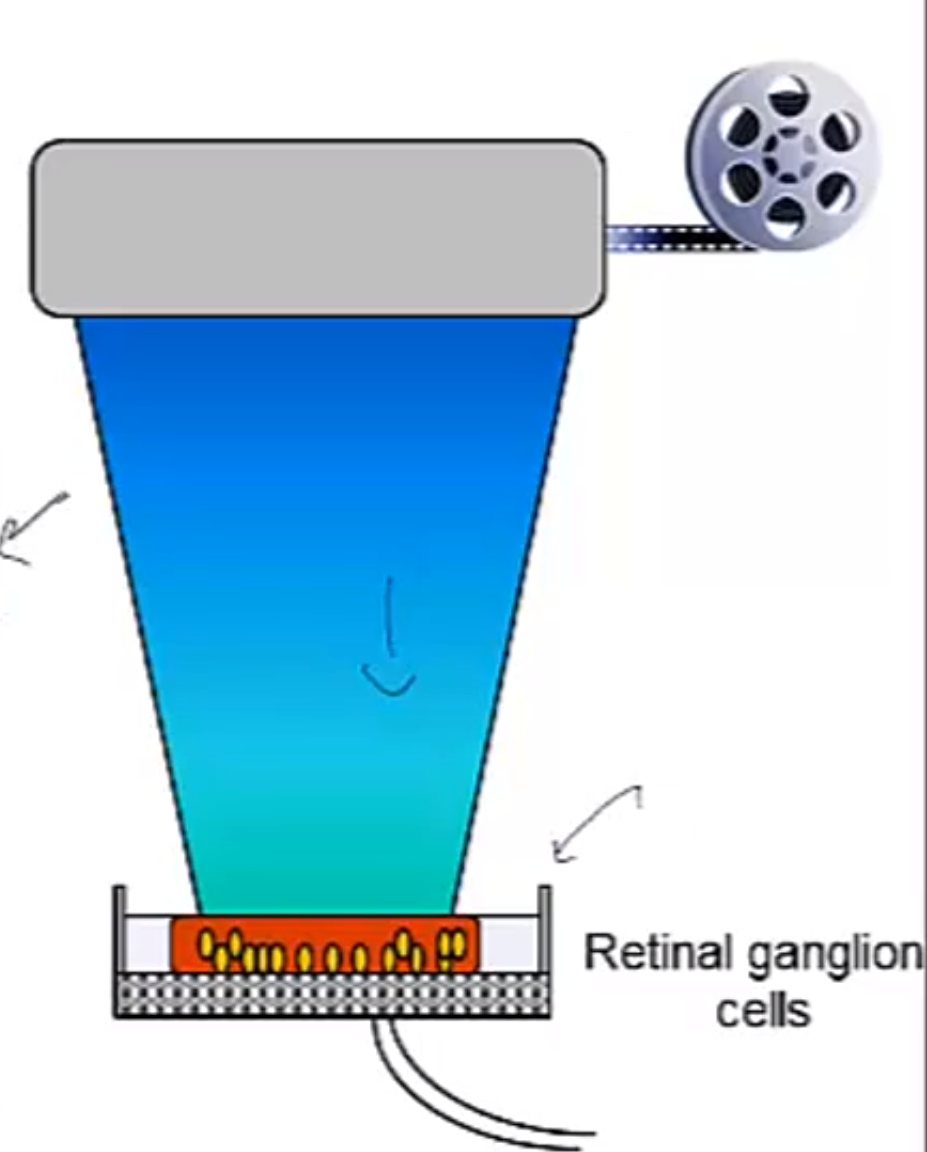
将视网膜神经节细胞用营养液养好，下面铺着记录每个细胞spike与否的electrode array，然后给他们放电影看:D

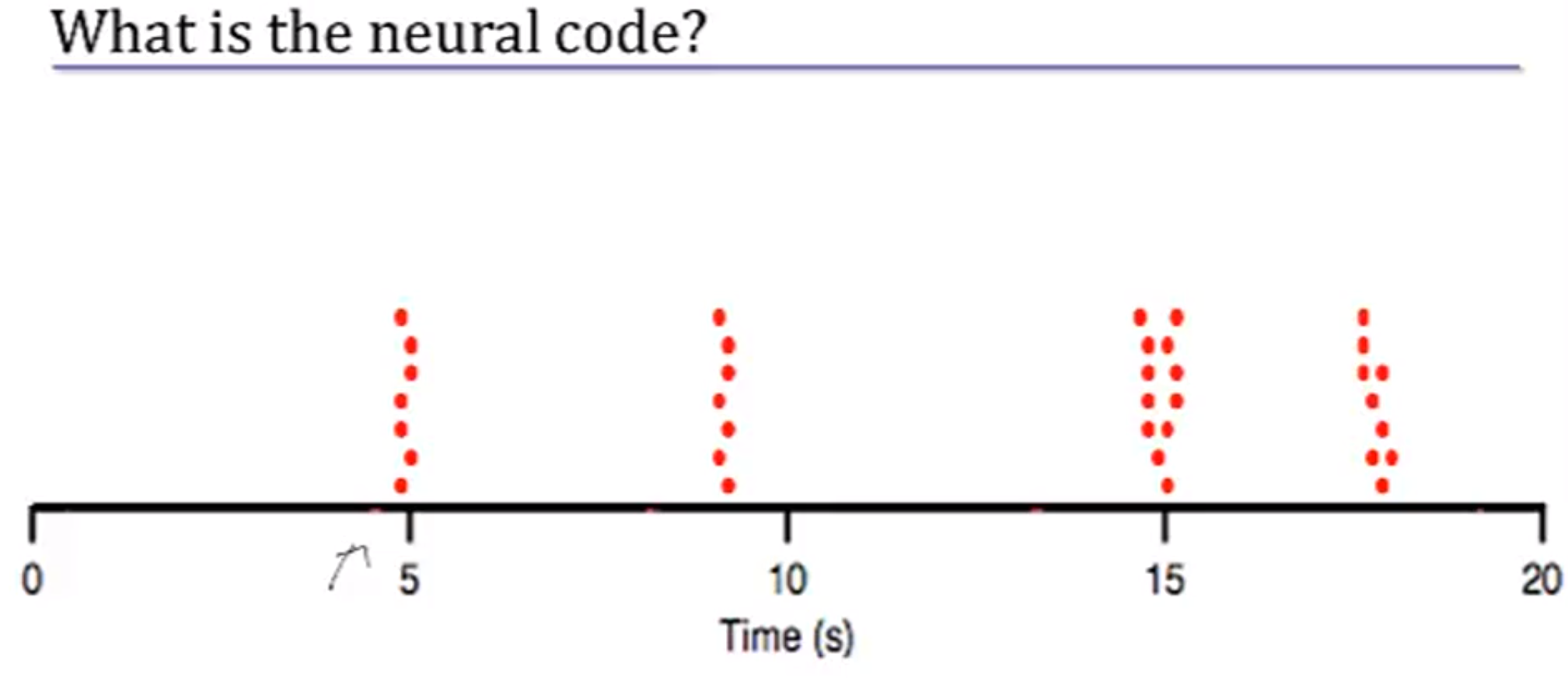
并且放很多遍，每遍都把该细胞兴奋的时间点标记出来，综合到上面一张图里，发现同一细胞兴奋点还真是差不多。。。像鱼吐泡泡一样。。。

然后把所有细胞的图绘制如下：

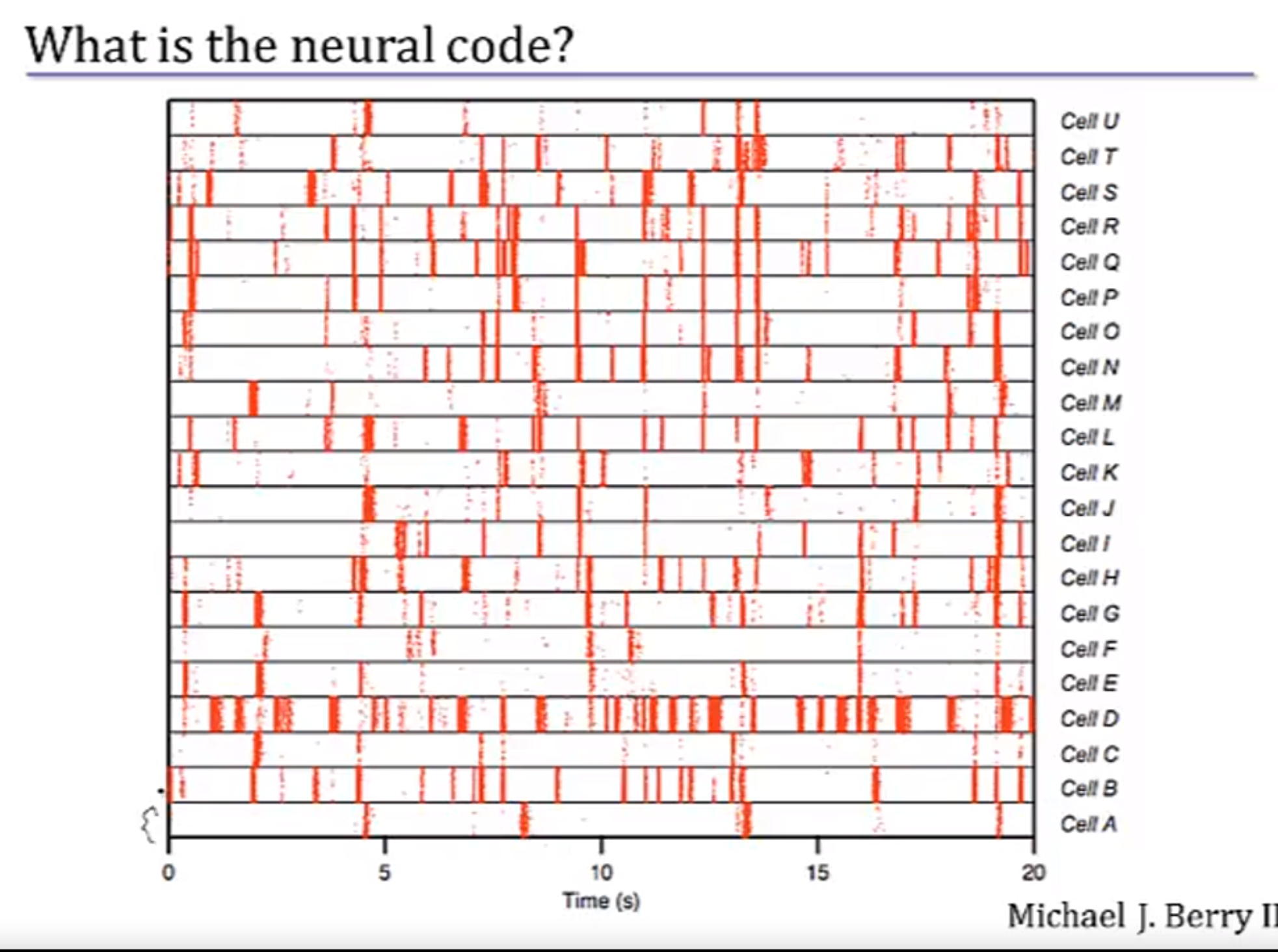
发现不同细胞都在对电影片段不同的细节进行编码（encoding)，传送到大脑更高级的部位里。每个细胞都像是一个小电脑在高速编程……把外界信息处理成大脑可以理解的电信号。amazing.

• Encoding: P(response

  stimulus)

  how does stimulus create a pattern of responses?

• Decoding: P(stimulus

  response)

  what do these response tell us about the stimulus?

• 用密码学来解释: 大脑接收到的外界的刺激是密文，大脑作出的反应是明文。

  从刺激预测反应是编码，从反应逆向刺激是译码

大脑对刺激反应的复杂度：

Geometric to semantic :从几何的到有语义的

interconnect: retina/LGN receives a massive amount of feedback from all these areas

​ expectation: what you think you’re looking at can shape what you actually see.(康德的认识论！)

​ (top-down effects)(semantic expectations)

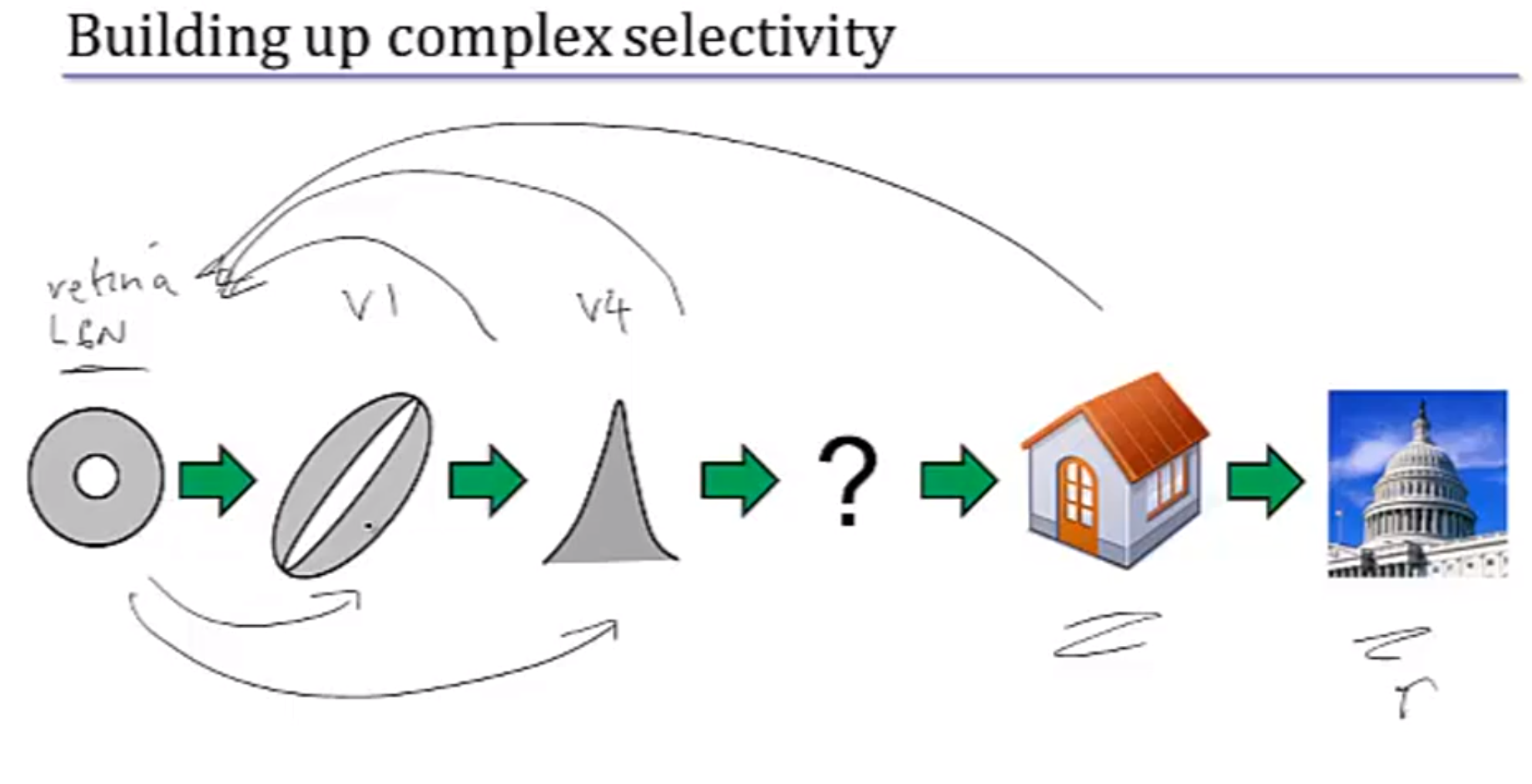
coding model

linear filtering

basic coding model: temporal filtering-时间滤镜

response: a single spike produced by a chosen neuron

$ r(t) $ : the probability seeing a spike at a certain time(firing rate)

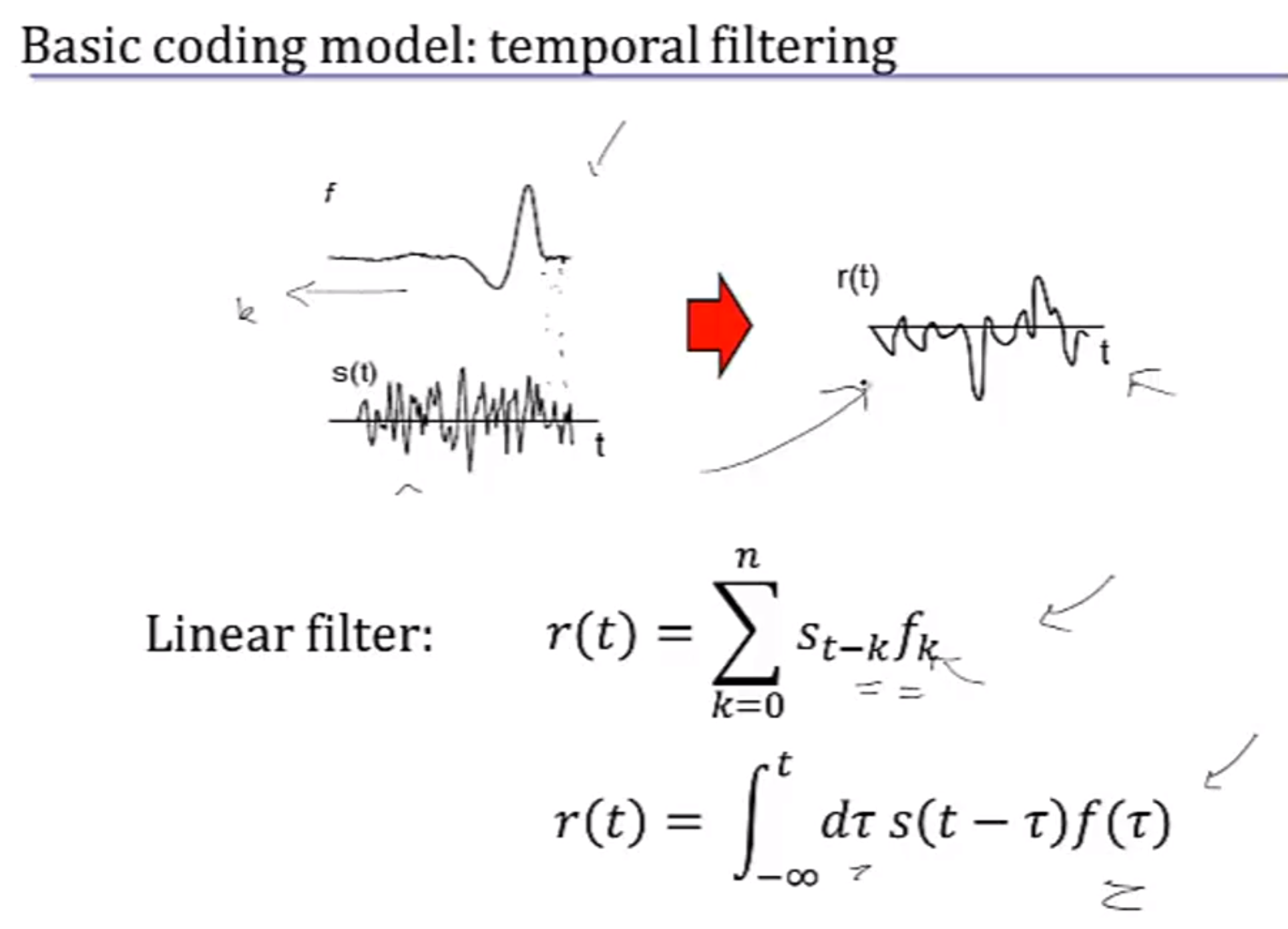
1. $ r(t) = {\phi} \,s(t)$ or $ r(t) = {\phi}\, s(t-{\tau})$
2. $ r(t) = \displaystyle\sum\limits_{k=0}^n\; s_{t-k}\, f_k$ or integral form: $ r(t) = \int_{-\infty}^t\, d\tau \, s(t-\tau) \, f(\tau)$ EG1： f(t) = 1/T EG2： f(t) = $ e^{t} $

basic coding model: spatial filtering-空间滤镜

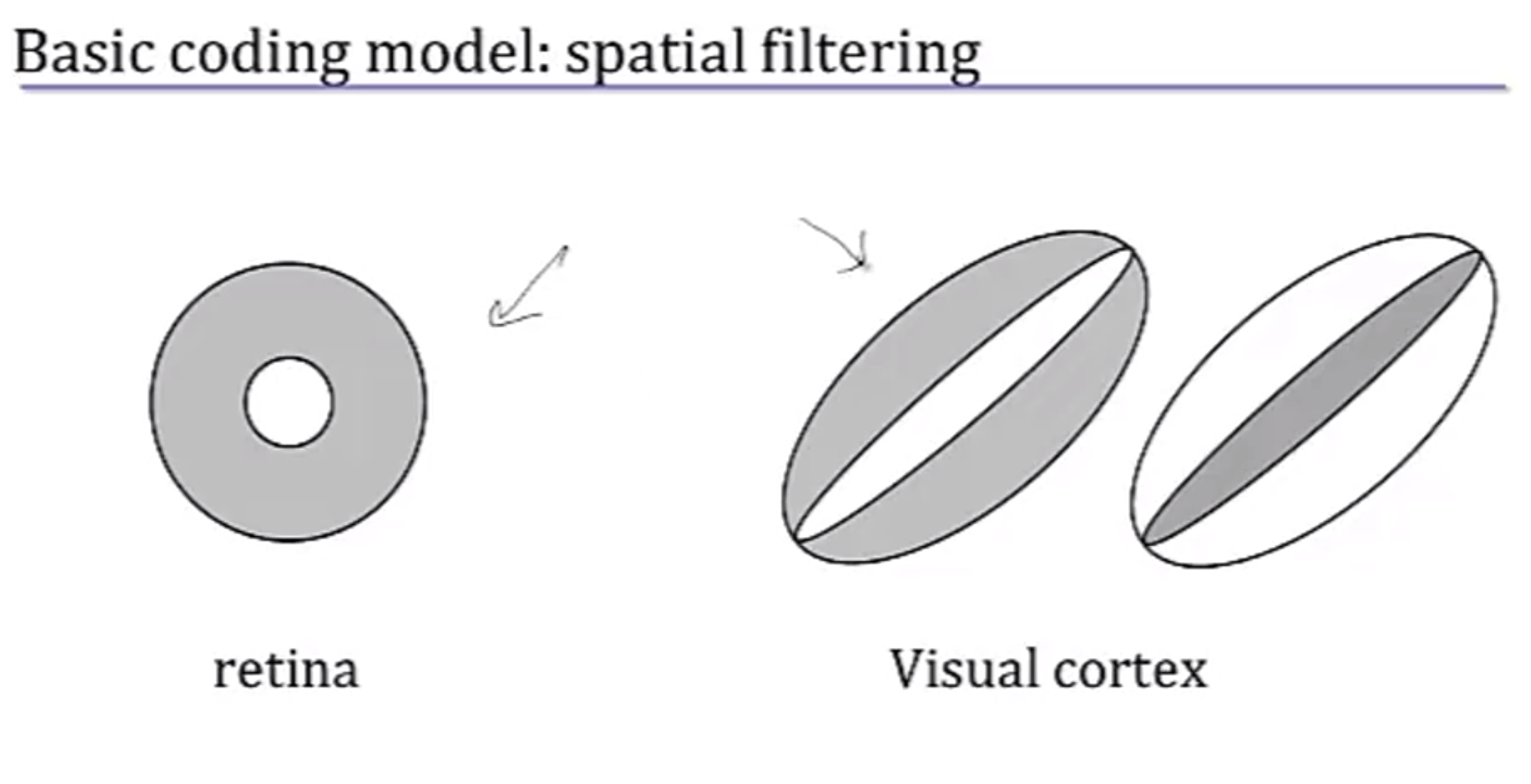
很容易推出对于r(t)描述的空间模型：

​ $ r(t) = \sum_{x’=-n,y’=-n}^{x’=n,y’=n}\, s_{x-x’,y-y’}\, f_{x’,y’}$

or r(t) = $ \int_{-\infty}^{\infty}\,dx’dy’s(x-x’,y-y’)f_{x’,y’} $

basic coding model: spatiotemporal filtering -时空滤镜

$ r_{x,y}(t) = \displaystyle\int!\int!\int dx’dy’d\tau \, f(x’,y’,\tau) s(x-x’,y-y’,t-\tau)$

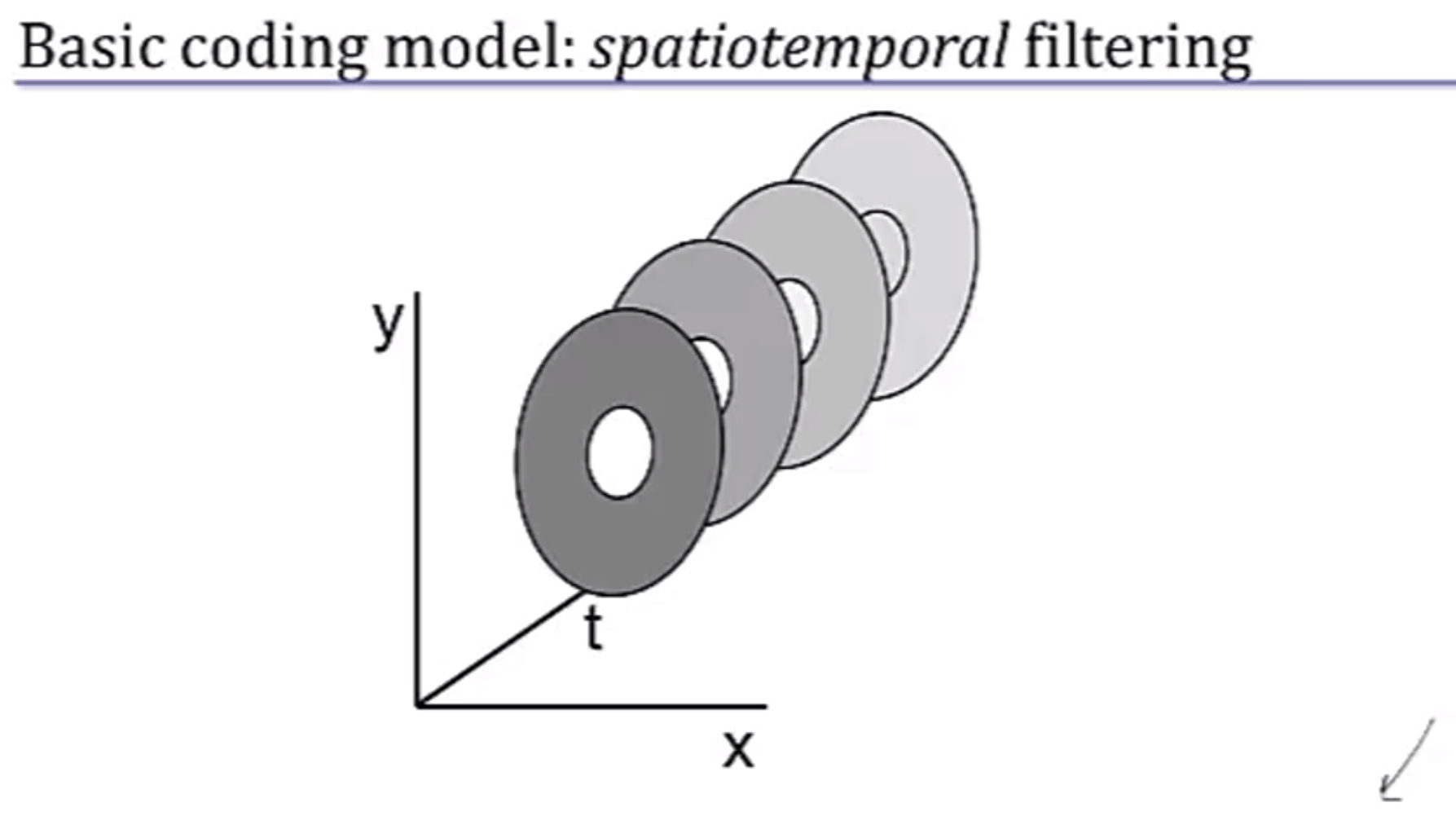
Standardized linear filtering

Linear filter & nonlinearity :$ r_{x,y}(t) = g\left(\int!\int!\int dx’dy’d\tau \, f(x’,y’,\tau) s(x-x’,y-y’,t-\tau)\right)$

Conclusion of basic coding model

1. r(t)肯定是一个跟s(t)有关的函数$r(t) = \phi s(t)$

2. 若假设刺激与空间位置无关，只与时间有关，即当前s(current)与前 T s的s(t)有关，并且是这些值的线性和，权重服从函数f(t)(比如$f(t) = e^{-t}$),那么r(t)就是s(t)与f(t)的卷积：

   $r(t) = \int_{-\infty}^t s(\tau)f(t-\tau)d\tau $ 离散的即：s(0)f(t)+s(1)f(t-1)+s(2)f(t-2)+…s(t)f(0)

3. 若假设刺激与时间无关，只与空间位置有关，即与感受野内的刺激有关，并且把感受野内的刺激作一个线性组合，权重或者过滤函数为f(x,y)，那么r(x,y)也同样是s(x,y)与f(x,y)的卷积：

   $r(x,y) = \int_{-\infty}^x\int_{-\infty}^ydx’dy’\, s(x’,y’)f(x-x’,y-y’) $

   这个像极了图象处理中的卷积，f即为卷积核。

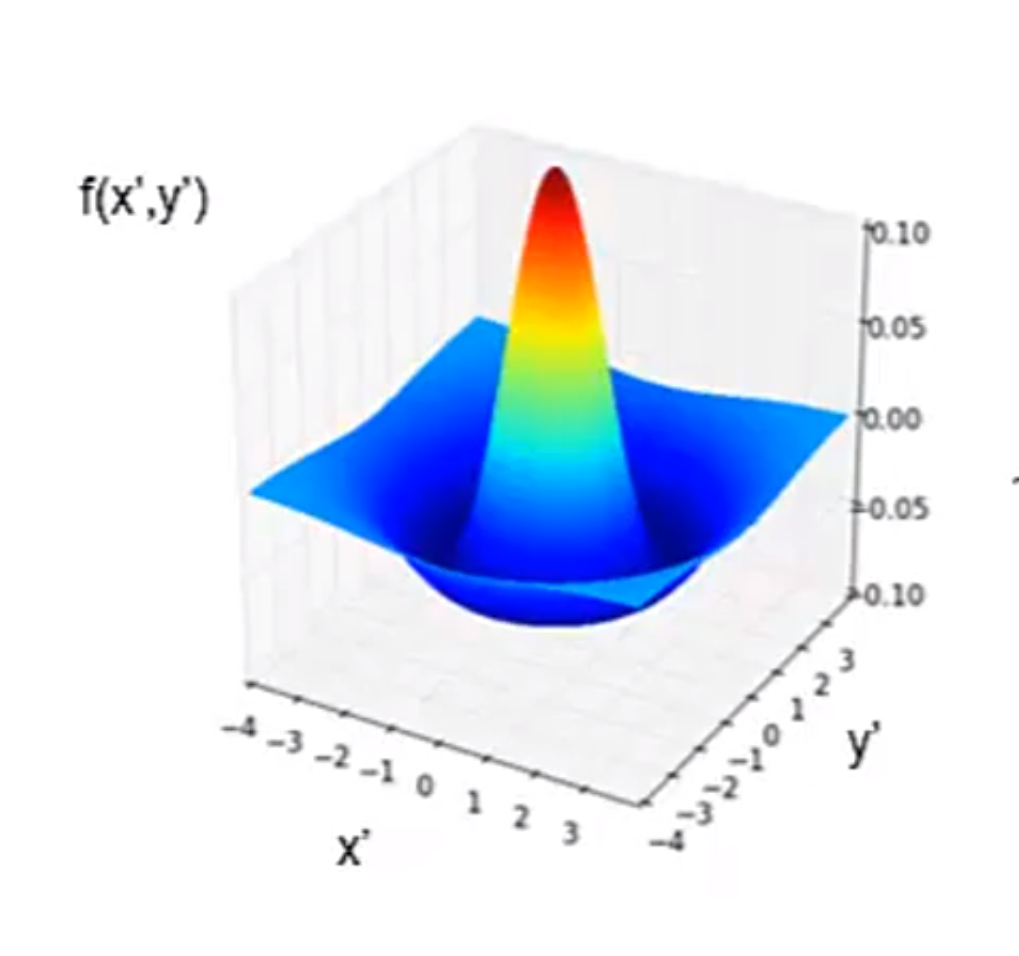
On-Feature 的 retinal ganglion cells 的 f(x,y)，表示当中心的像素是亮点时，f(0,0)*s(0,0)会是个很大的正数，提升了其r(t)即产生刺激的概率；当周围的像素是暗点时，f和s相乘会是一个绝对值比较小的负数，也相当于提升了r(t)，否则，当周围也是亮点，由于该点的f(x,y)是负值，那么会降低细胞兴奋的概率。

1. 最后我们将时空综合起来，得到一个相对合理的模型，同时考虑了时间和空间对r(t)的影响,并且加入非线性的g(x)使概率控制在合理的范围内(0-1)，相当于对其标准化。

   $ r_{x,y}(t) = g\left(\int!\int!\int dx’dy’d\tau \, f(x’,y’,\tau) s(x-x’,y-y’,t-\tau)\right)$

Feature Selection

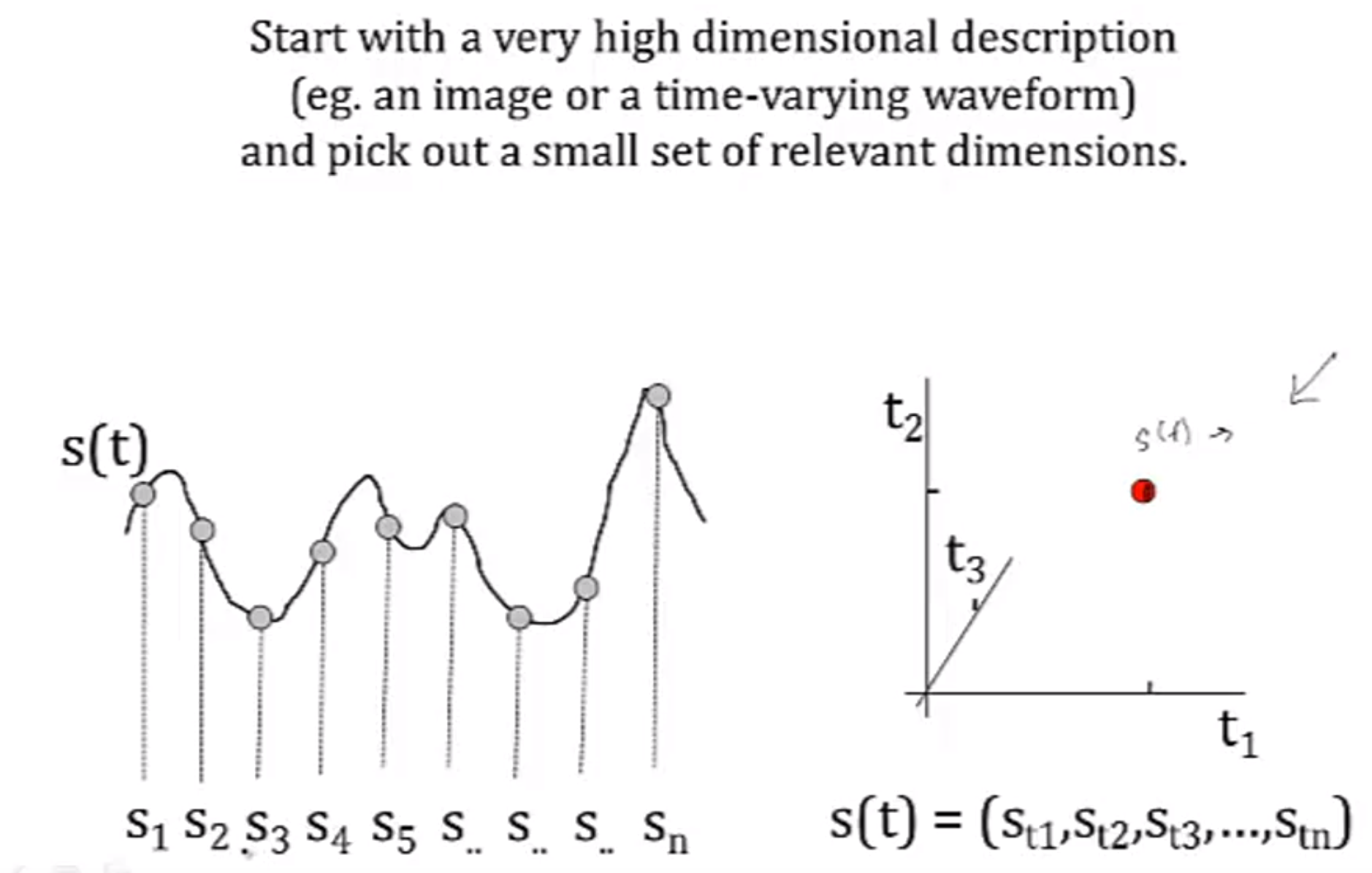
现在有一个问题：每一个样本点的数据量太大，我们需要把多余的，相关性强的数据整合成精简的数据

• Gaussian white noise

vacabulary list:
  - calcium n. 钙
  - florescent / flourescent a. 荧光的
  - florescent property 荧光物质
  - clamp 夹具 a device holds two things firmly together
  - integral 积分的
  - map...onto  map the filtered stimulus onto the firing rate.